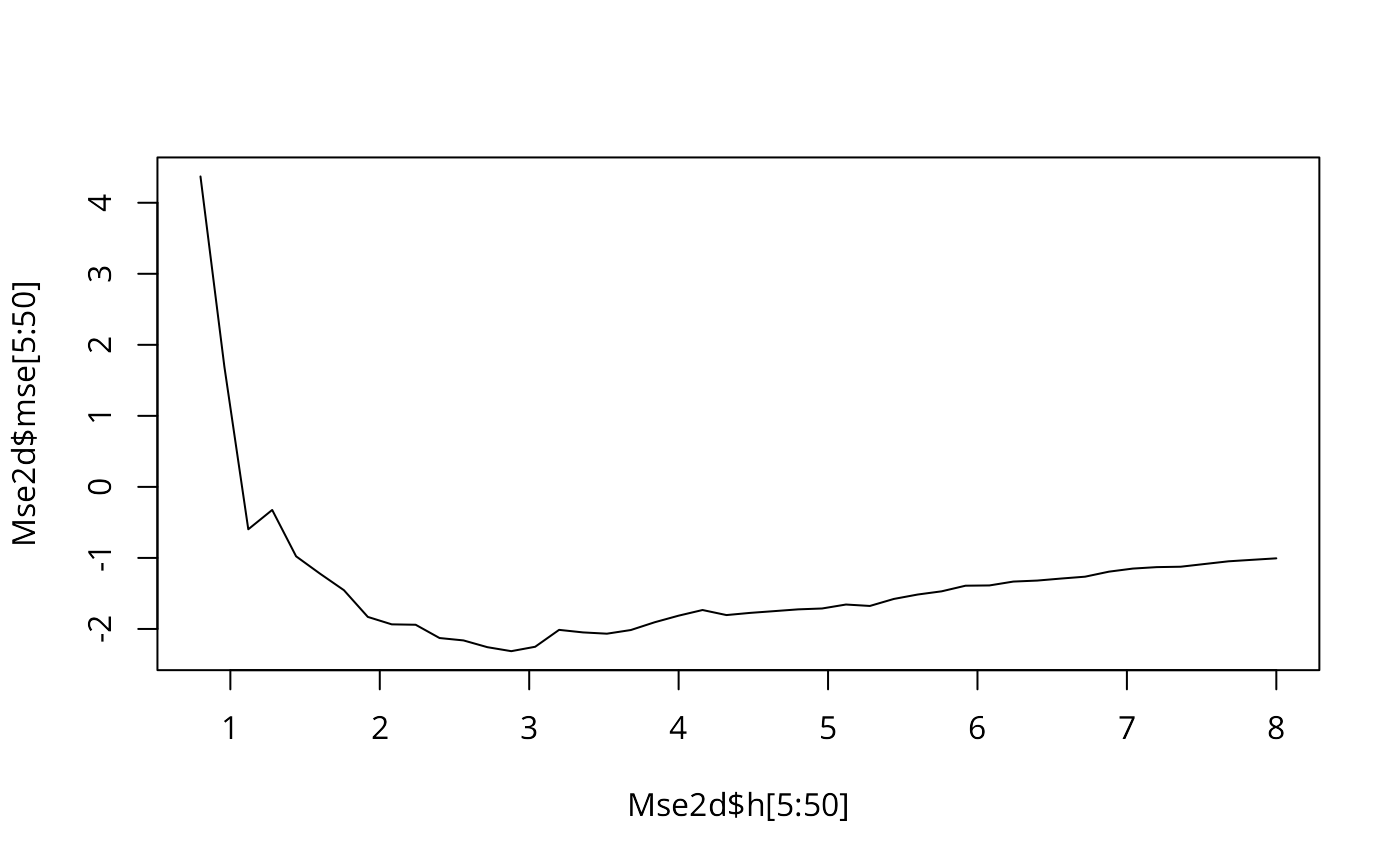
Mean Square Error for a Kernel Smoothing

Estimate the Mean Square Error for a Kernel Smoothing.

mse2d(pts,poly,nsmse, range)

Arguments

pts

A set of points.

poly

A polygon containng the points.

nsmse

Number of steps of h at which to calculate the mean square error.

range

Maximum value of h for calculating the mean square error.

Value

A list with two components, $h and $mse. These vectors store corresponding values of the mean square error at values of the kernel smoothing parameter, h. The value of h corresponding to the minimum value of $mse

can be passed to kernel2d as the optimum smoothing parameter.

See also

kernel2d

References

Berman M. & Diggle P.J. (1989) Estimating Weighted Integrals of the Second-Order Intensity of a Spatial Point Pattern. J. R. Statist Soc B 51 81--92; Rowlingson, B. and Diggle, P. 1993 Splancs: spatial point pattern analysis code in S-Plus. Computers and Geosciences, 19, 627-655; the original sources can be accessed at: https://www.maths.lancs.ac.uk/~rowlings/Splancs/. See also Bivand, R. and Gebhardt, A. 2000 Implementing functions for spatial statistical analysis using the R language. Journal of Geographical Systems, 2, 307-317.

Examples

data(bodmin)
Mse2d <- mse2d(as.points(bodmin), bodmin$poly, nsmse=50, range=8)
plot(Mse2d$h[5:50],Mse2d$mse[5:50], type="l")